Tag 2: Blender Car Modeling

16. April 2018 Ralf Dreiundzwanzig Allgemein Schlagwörter: 3D-Modelling, Car 0 Kommentare

Dreidimensionale (3D-)Modelle stellen einen physischen Körper dar, indem sie eine Sammlung von Punkten im 3D-Raum verwenden, die durch verschiedene geometrische Elemente wie Polygone, Linien, gekrümmte Flächen usw. verbunden sind. Da es sich um eine Sammlung von Daten (Punkte und andere Informationen) handelt, können 3D-Modelle von Hand, algorithmisch (prozedurale Modellierung) oder gescannt werden. Ihre Oberflächen können durch Textur-Mapping weiter definiert werden.

Sie haben es eilig? Dann speichern Sie diesen Blogartikel von R23 als PDF

Brauchen Sie den Inhalt dieses Artikels "Tag 2: Blender Car Modeling" schnell und bequem? Dann speichern Sie ihn doch einfach als PDF!

Download PDF

3D-Modelle werden überall in der 3D-Grafik eingesetzt. Ihre Verwendung geht der weit verbreiteten Verwendung von 3D-Grafiken auf Personalcomputern voraus. Viele Computerspiele verwendeten vorgerenderte Bilder von 3D-Modellen als Sprites, bevor Computer sie in Echtzeit rendern konnten. Der Designer kann dann das Modell in verschiedene Richtungen und Ansichten sehen, dies kann dem Designer helfen, zu sehen, ob das Objekt im Vergleich zu seiner ursprünglichen Vision erstellt wurde. Das Design auf diese Weise zu sehen, kann dem Designer/Unternehmen helfen, Änderungen oder Verbesserungen am Produkt herauszufinden.

Heute werden 3D-Modelle in den verschiedensten Bereichen eingesetzt. Die medizinische Industrie verwendet detaillierte Modelle von Organen; diese können mit mehreren 2D-Bildschnitten aus einem MRT- oder CT-Scan erstellt werden. Die Filmindustrie verwendet sie als Figuren und Objekte für animierte und reale Filme. Die Videospielindustrie nutzt sie als Assets für Computer- und Videospiele. Die Wissenschaft nutzt sie als hochdetaillierte Modelle chemischer Verbindungen. Die Architekturindustrie nutzt sie, um vorgeschlagene Gebäude und Landschaften anstelle von traditionellen, physischen Architekturmodellen zu demonstrieren. Die Ingenieurgemeinschaft nutzt sie für die Entwicklung neuer Geräte, Fahrzeuge und Strukturen sowie für eine Vielzahl weiterer Anwendungen. In den letzten Jahrzehnten hat die geowissenschaftliche Gemeinschaft damit begonnen, geologische 3D-Modelle als Standardverfahren zu konstruieren. 3D-Modelle können auch die Grundlage für physikalische Geräte sein, die mit 3D-Druckern oder CNC-Maschinen gebaut werden.

Wir visualisieren Ideen!

R23 ist Ihre Digitalagentur für Virtual & Augmented Reality. Wir investieren in immersive Technologien wie Augmented Reality und künstliche Intelligenz, die die Grundlage für die Art und Weise sein werden, wie wir in Zukunft online einkaufen. Mit neuen visuellen Entdeckungstools helfen wir Käufer:innen, neue Produkte zu finden, und mit AR-Erlebnissen helfen wir Menschen, Artikel zu visualisieren, bevor sie sie kaufen.

Fotorealistische Visualisierungen und 3D-Animationen lassen sich schnell und kostengünstig erzeugen und in Ihrem Online-Shop veröffentlichen.

Beispiel 3D-Modell Stilvoll. Modern. Zeitlos. Couch

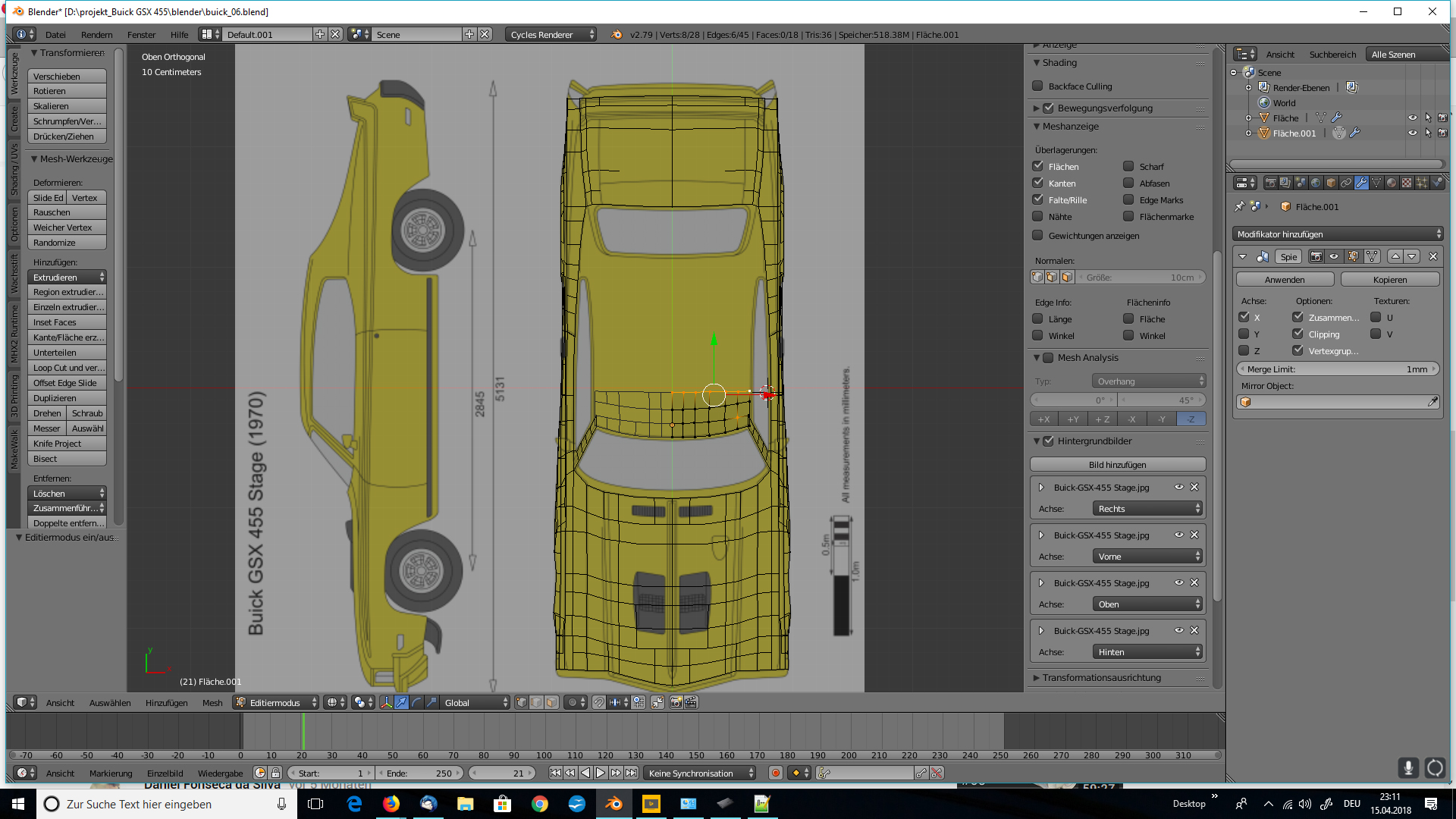
Im blog.r23.de könnt Ihr die 3D-Visualisierung von einem Oldtimer nach Blaupausen verfolgen.

Über meinen Online Shop könnt Ihr später 3D-Modelle kaufen oder 3D-Modelling von Oldtimer, Sportwagen oder Concept Cars erstellen lassen. Den Weg zu dem Angebot könnt Ihr im Blog verfolgen.
Ich freue mich über Anregungen und die ersten Aufträge. Ich benötige nur die Frontansicht, Aufsicht, Rückseite, Seite als Zeichnung oder Foto von deinem Auto und wenige Tage später erhältst Du von mir Deine 3D-Grafik.

Auch am Tag zwei Stand die Polygonale Modellierung auf der To-do-Liste.

Polygonale Modellierung

In der 3D-Computergrafik ist die Polygonmodellierung ein Ansatz zur Modellierung von Objekten durch Darstellung oder Annäherung ihrer Oberflächen mit Hilfe von Polygonen. Die polygonale Modellierung eignet sich gut für das Scanline-Rendering und ist daher die Methode der Wahl für Echtzeit-Computergrafiken.

Das Grundobjekt der Netzmodellierung ist ein Scheitelpunkt, ein Punkt im dreidimensionalen Raum. Zwei durch eine gerade Linie verbundene Eckpunkte werden zu einer Kante. Drei Eckpunkte, die durch drei Kanten miteinander verbunden sind, definieren ein Dreieck, das das einfachste Polygon im euklidischen Raum ist. Komplexere Polygone können aus mehreren Dreiecken oder als ein einziges Objekt mit mehr als 3 Eckpunkten erzeugt werden. Vierseitige Polygone (allgemein als Vierecke bezeichnet) und Dreiecke sind die am häufigsten verwendeten Formen bei der Polygonmodellierung. Eine Gruppe von Polygonen, die durch gemeinsame Eckpunkte miteinander verbunden sind, wird allgemein als Element bezeichnet. Jedes der Polygone, aus denen ein Element besteht, wird als Face bezeichnet.

In der euklidischen Geometrie bestimmen drei beliebige nicht-kollineare Punkte eine Ebene. Aus diesem Grund bewohnen Dreiecke immer nur eine Ebene. Dies gilt jedoch nicht unbedingt für komplexere Polygone. Die flache Natur der Dreiecke macht es einfach, ihre Oberflächennormale zu bestimmen, einen dreidimensionalen Vektor senkrecht zur Oberfläche des Dreiecks. Oberflächennormale sind für die Bestimmung des Lichttransports beim Raytracing nützlich und sind ein wichtiger Bestandteil des beliebten Phong-Shading-Modells. Einige Rendering-Systeme verwenden Vertex-Normale anstelle von Flächennormalen, um ein besser aussehendes Beleuchtungssystem auf Kosten von mehr Verarbeitung zu erzeugen. Beachte, dass jedes Dreieck zwei Flächennormale hat, die in entgegengesetzte Richtungen zeigen. In vielen Systemen gilt nur eine dieser Normen als gültig - die andere Seite des Polygons wird als Rückwand bezeichnet und kann je nach Wunsch des Programmierers sichtbar oder unsichtbar gemacht werden.

Viele Modellierungsprogramme setzen die geometrische Theorie nicht strikt durch, z.B. ist es möglich, dass zwei Scheitelpunkte zwei unterschiedliche Kanten haben, die sie miteinander verbinden und genau die gleiche räumliche Position einnehmen. Es ist auch möglich, dass zwei Scheitelpunkte an den gleichen Raumkoordinaten oder zwei Flächen an der gleichen Stelle existieren. Solche Situationen sind in der Regel nicht erwünscht und viele Pakete unterstützen eine Auto-Cleanup-Funktion. Wenn keine automatische Bereinigung vorhanden ist, müssen sie jedoch manuell gelöscht werden.

Eine Gruppe von Polygonen, die durch gemeinsame Eckpunkte verbunden sind, wird als Mesh bezeichnet. Damit ein Mesh attraktiv erscheint, wenn es gerendert wird, ist es wünschenswert, dass es sich nicht selbst schneidet, d.h. keine Kante durch ein Polygon geht. Eine andere Betrachtungsweise ist, dass sich das Mesh nicht selbst durchbohren kann. Es ist auch wünschenswert, dass das Netz keine Fehler wie doppelte Ecken, Kanten oder Flächen enthält. Für einige Zwecke ist es wichtig, dass das Mesh ein Vielfaches ist - das heißt, dass es keine Löcher oder Singularitäten enthält (Stellen, an denen zwei verschiedene Abschnitte des Netzes durch einen einzigen Scheitelpunkt verbunden sind).

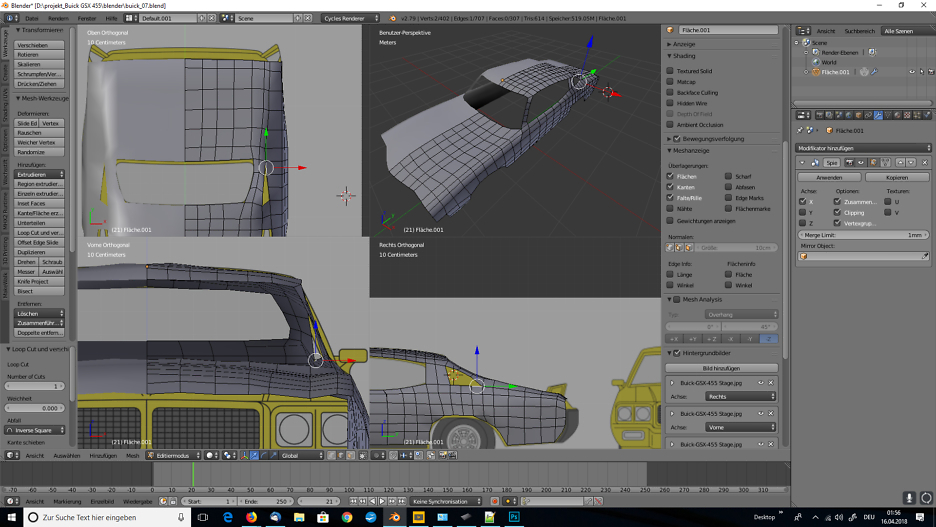
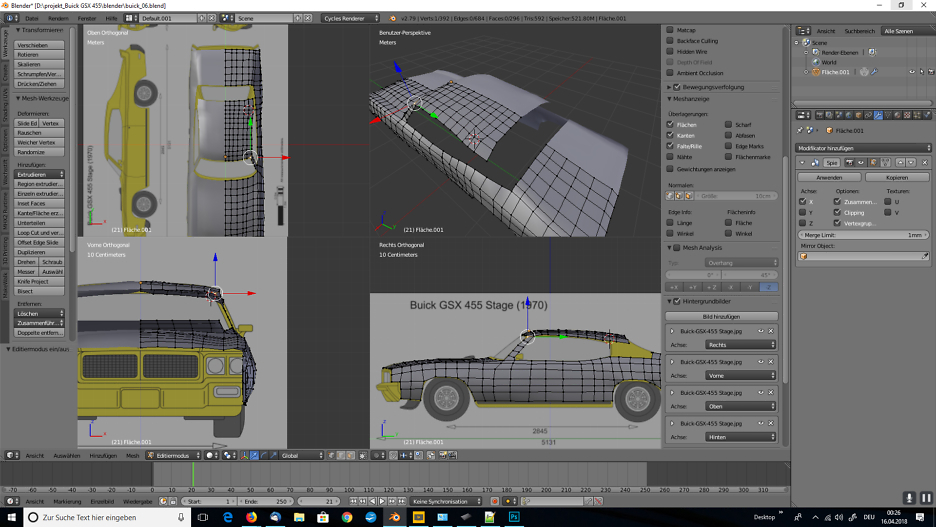
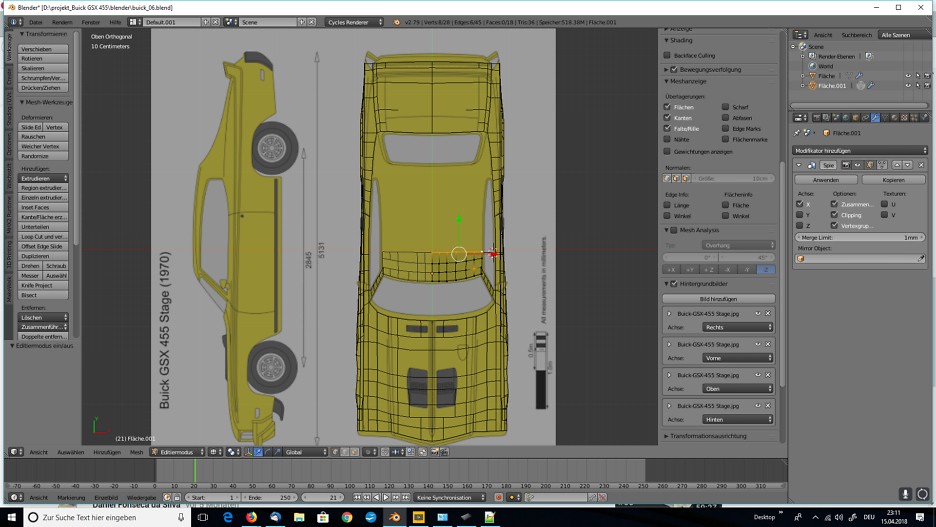
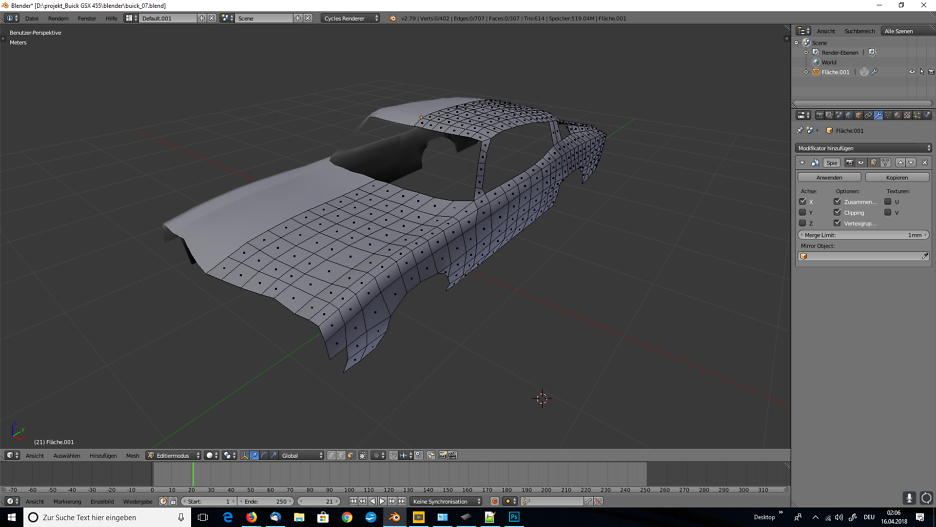
Für eine grössere Ansicht klicke auf ein Bild

Jetzt bist du gefragt!

Hast du Anregungen, Ergänzungen, einen Fehler gefunden oder ist dieser Beitrag nicht mehr aktuell? Dann freue ich mich auf deinen Kommentar.

Du kannst diesen Beitrag natürlich auch weiterempfehlen. Ich bin dir für jede Unterstützung dankbar!

Wie können wir Ihnen helfen?

Wir unterstützen Sie bei der Umsetzung Ihres Augmented Reality (AR) oder Virtual Reality (VR) Projektes! Egal ob Produktfotografie, 3D-Scan-Service, 3D-Visualisierung oder fertige 3D-Modelle für AR/VR – wir beraten Sie persönlich und unverbindlich.

Wünschen Sie ein individuelles Angebot auf Basis Ihrer aktuellen Vorlagen, nutzen Sie einfach unser Anfrageformular.